Grafo no orientado	Terna G=(V,A,Phi)	G=()
Dónde V:	Elementos de G o Extremos	V:{}
Dónde A	Aristas de G	G:{}
Phi	Función que asigna a cada arista un par no ordenado de vértices o extremos. Phi(a)=(v1,v2)	Phi(a)=?
Incidente	Si una arista es extremo de un vértice.	Phi(a1):(v1,v2)
Adyacente	Dos aristas o vertices son adyacentes cuando existe un vértice o arco que los une respectivamente.	a y v.
Grado de un vertice	Número de aristas que inciden en un vértice.	G(?)=?
Vértice aislado	Si G(v)=0	v=
Vértice pendiente	Si G(v)=1	v=?
Lazo	Arista cuyos extremos coinciden.	a(?)=a(?)
Aristas paralelas	Mismo vértice inicial y mismo vértice final.	2 a son paralelas cuando
Cadena	Sucesión finita de aristas.	(?1,?2,?3)
Longitud de una cadena	Cantidad de aristas que la componen.	l(c)= N° de a o N° de v?
Cadena sencilla	No se repiten aristas.	aristas o vertices?
Cadena elemental	No se repiten vertices.	Aristas o vertices?
Ciclo	Coinciden vértice inicial y vértice final.	Cadena dónde...
Grafo simple	Grafo sin lazos ni aristas paralelas.	Sin vueltas
Grafos orientados	Terna G:(V,A,Phi) dónde A son los arcos que unen los vertices y Phi un par ordenado que indica los extremos de los mismos.	Bien completa.
Rizo o bucle	Arco dónde el vértice inicial coincide con el vértice final.	Vértice inicial o vértice final?
Arcos estrictamente paralelos	tienen mismo vértice inicial y mismo vértice final.	2 arcos son estrictamente paralelos cuando...
Arcos adyacentes	Tienen un vértice que los une	Dos a son adyacentes cuando...
Vertices adyacentes	Tienen un arco que los une	Dos v son adyacentes cuando...
Arcos incidentes	Positiva: el vértice es el origen del arco. Negativa: el vértice es el extremo del arco. Phi(a)=(vi,vj) ^ vi =\= vj. a1 incide positivamente en vi y negativamente en vj.	Si dos vertices son distintos, un arco incide positivamente en un vértice si... E incide negativamente si...
Grados	Total: Suma de g+ y g-. Neto: Diferencia de g+ y g-.	Grado total y grado neto.
Propiedades de grados de vertices.	La sumatoria de los grados positivos de los vertices de un grafo es equivalente a la suma de los grados negativos y por consecuente al número de arcos del grafo. La sumatoria de los grados totales de los vertices de un grafo es equivalente a el doble del total de arcos del grafo. La sumatoria de los grados netos de un vértice es igual a 0.	Sumatoria g+(v) = Sumatoria g-(v)? sumatoria gt(v) = \|A\|? Sumatoria gn(v) =?
Caminos	Camino: Secuencia de arcos. Sencillo: no se repiten arcos. Elemental: no se repiten vertices. circuito: coinciden vi y vf. Sencillo: no se repiten arcos. Elemental: No se repiten vertices excepto el vi y vf.	Camino? sencillo? elemental? circuito?
Matriz de adyacencia de vertices	Define la adyacencia de los vertices en una matriz ordenada o no ordenada.	¿Que define?
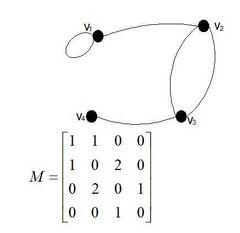
Elementos matriz de adyacencia	Se crea una matriz con un orden de nxn, siendo n el número de elementos del grafo. Se representa en cada fila y en cada columna la posibilidad de adyacencia para cada elemento.
Para cada matriz de adyacencia se cumple que	No Orientada: La suma de los elementos distintos de 0 de la matriz es igual a 2*\|A\|. Siendo A el número de aristas. Orientada: La suma de los elementos distintos de 0 de la matriz es igual al número de arcos del grafo.	Grafo Orientado Grafo no orientado
Longitud de una cadena	Teorema: Si M es la matriz de adyacencia de un grafo G, entonces el elemento mij =/= 0 de la amatriz M^lambda, lambda pertenenciente a N, indica la existencia de por lo menos, un camino de longitud lambda entre vi y vj. Corolario: En un grafo existe por lo menos un camino de longitud lambda si M^lambda =/= Matriz nula.	Existe una cadena de longitud lambda si...
Matriz de incidencia	Es una matriz rectangular de clase nxr : n=Nro de Vertices; r=Nro de aristas.	Mnxr?
Teorema de Matriz de Incidencia	No orientado: Cada columna tiene dos 1 únicamente, el resto 0. La suma de los elementos de una fila es igual al grado del vértice en cuestión. Orientado: Cada columna tiene un 1 y un -1, el resto 0. La suma de los elementos de una fila puede ser: Grado neto al sumar normalmente. Grado total al sumar los valores absolutos.	Orientado, No orientado
Subgrafos	El grafo S=(V1, A, Phi1) es un subgrafo de G=(V, A, Phi) si se verifica: 1) V1 pertenece a V 2) A1 pertenece a A 3) Phi1 es una restricción de Phi a A1.	Cuando es un subgrafo?
Subgrafo minimal	Subgrafo S de G que goza de propiedad P si ningun subgrafo de S puede gozar de la propiedad de P	Subgrafo S de G
Subgrafo Maximal	si ningún subgrafo estrictamente mayor que S (es decir con más vértices y/o aristas) goza de la propiedad P.	un subgrafo S de G que goce de una propiedad P
Subgrafo cobertor	si contiene a todos los vértices de G	Subgrafo S de G que
Obtener subgrafo y casos particulares.	Se obtiene suprimiendo vertices y/o aristas. Casos particulares * Subgrafo generado por subconjunto de vertices W: subgrafo que tiene a W cono conjunto de vertices y cuyo conjunto de aristas está formado por todas las aristas del grafo original G que tienen ambos extremos en W.	Subgrafo generado por subconjunto. Subgrafo minimal.
Grafo complementario	Sea g un Grafo, se llama CG al grafo que tiene el mismo conjunto de vertices de G y cuyo conjunto de aristas son las que le faltan a G para ser completado.	CG=(V,A',Phi')
Conexidad No orientada	Un grafo G es conexo si dados cualesquiera dos vertices v y w en G, existe una cadena de v a w. "En el grafo G=(V, A, Phi), definimos la siguiente relación: 'El vértice vj es alcanzable desde el vértice vi si existe una cadena que va de vi a vj'"	G(V)={v,w}
Componente conexo de grafo no orientado	es el grafo generado por v sub n y todos los vértices que están unidos a v sub n por medio de una cadena.	subgrafo generado por...
Conexidad simple	Sea G=(V,A,Phi), es conexo si para todo par de vértices distintos vi =/= vj del mismo existe un camino que los une por lo menos en un sentido.	Si dos vértices son distintos...
Fuertemente conexo	un grafo orientado G es fuertemente conexo cuando todo par de vértices distintos del mismo está unido en ambos sentidos por un camino.	Si existe...
Componente conexa	todo subgrafo maximal conexo. (Mayor numero de aristas y vértices que cumple la condición)	es todo...
Componente fuertemente conexa	Todo subgrafo maximal fuertemente conexo.	es todo subgrafo...
Matriz de conexión	es la matriz C=\|cij\| de dimensión mxm donde se coloca 1 si existe una trayectoria de un vértice al otro o 0 en caso contrario.	Dado un grafo G de m vértices
Determinación de conexidad por matríz.	En caso de tener un elemento 0 en la matriz el grafo no es fuertemente conexo, para comprobar la conexidad se debe realizar la suma booleana de la misma con su traspuesta.	Que operación debemos hacer con la matriz?
Obtener componentes fuertemente conexas de la matriz	Para ver las componentes fuertemente conexas debemos hacer el producto booleano de C y C transpuesta elemento a elemento. Luego realizar operaciones elementales para obtener un nro de bloques y este nro será la cantidad de cfc.	Que operación debemos hacer con la matriz?
Recorridos Hamiltoniano	Cadena: Recorre todos los vértices del grafo sin repetirlos. Circuito: Recorre todos los vértices del grafo repitiendo únicamente el final.	vi =/= vj, para todo i, j.
Recorridos Eulerianos	Cadena: Recorre todas las aristas o arcos del grafo sin repetirlos. Circuito: Recorre todas las aristas o arcos del grafo sin repetirlos.	ai =/= aj, para todo i, j.
Teoremas de recorridos eulerianos.	* G admite admite una cadena Euleriana sí y sólo sí es conexo y el número de vértices de grado impar es cero o dos. * G admite ciclo Euleriano sí y sólo sí es conexo y todos sus vértices son de grado par. * G orientado admite un circuito Euleriano sí y sólo sí el grado neto de los vértices es cero.	Cuando admiten recorridos eulerianos?
ARBOL	Grafo conexo y acíclico

Descubre

Crear Tarjetas

Acerca de Nosotros

Explore Tarjetas

Comparta este Set de Tarjetas de Aprendizaje

Matemática Discreta - Grafos

Cómo estudiar sus tarjetas

Rango de Cartas a estudiar

51 Cartas en este set