Teorema 1.1:	Supongamos que: •g es una función continua. •{Pn}(n=0–>∞) es una sucesión generada por iteración de punto fijo. Si lim(n–>∞) Pn=P, entonces P es un punto fijo de g(x)	2 condiciones para que P sea PF de g(x)
Teorema 1.2: Existencia y unicidad	Supongamos que g es continua en el intervalo [a, b] •Existencia: si y=g(x) verifica que y E [a, b] para cada x E [a, b], entonces g tiene un punto fijo en [a, b]. En otras palabras, si la imagen de g está contenida en el intervalo, entonces existirá un punto fijo en dicho intervalo. Unicidad: si g'(x) está definida en (a,b) y \|g'(x)\| < 1 para todo x E (a, b), entonces g tiene un único punto fijo P en [α, b]
Teorema 1.3: PF converge/diverge	Supongamos que: •g, g' son continuas en[a, b]. •K es una constante positiva. •Po E [a, b] para todo x perteneciente a dicho intervalo. Entonces hay un punto fijo P de g en [a, b]. a. Si \|g'(x)\|≤K<1para toda x E [a, b], entonces P es el único punto fijo de g en [a, b] y la iteración pn = g(Pn-1) converge a dicho punto fijo. En este caso, se dice que P es un punto fijo atractivo. b. Si lg'(P)l>1 y po≠P entonces la iteración pn = g(pn-1) no converge al punto fijo. En este caso, P es un punto fijo repulsivo y la iteración diverge.
Teorema 2.1 conveniencia del método de la bisección
Teorema 4.1: Teorema de Newton Raphson
Definición: orden de convergencia el método
Teorema 4.2: Orden de convergencia del método NR
Teorema 4.3: convergencia local del método de Newton raphson
Error realizado en método PF
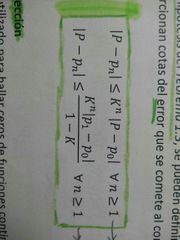